Erkennen und Erkunden universeller Strukturen, um mehr über die Welt um uns herum zu erfahren, ist eine wesentliche Antriebskraft der Wissenschaft. Karl Popper drückte dies so aus: "Wenn es das Ziel der Wissenschaft ist, zu erklären, ist es auch ihr Ziel, das zu erklären, was bisher als Erklärungsgrund akzeptiert wurde, wie etwa ein Naturgesetz. Somit erneuert sich die Aufgabe der Wissenschaft ständig selbst. Wir könnten ewig weitermachen und zu Erklärungen von immer höherem Allgemeinheitsgrad und Universalität gelangen …"

Für Naturwissenschaften ist das plausibel, aber was sind solche Erklärungsgründe oder Naturgesetze in den Finanz- und Wirtschaftswissenschaften? Universalität mag hier überraschend klingen, da Finanzmärkte keinen "Naturgesetzen" folgen. Doch es gibt universelle Marktstrukturen, die zumindest über gewisse Zeit und Märkte hinweg gelten und durch statistisch messbare Größen sichtbar gemacht werden können.

Stabilität der Marktkapitalverteilungskurven

Dies lässt sich gut anhand von zwei Beispielen veranschaulichen: erstens die Stabilität der Marktkapitalverteilungskurven über die Zeit, und zweitens die sogenannte "pfadabhängige Volatilität". Das erste Beispiel ist in folgender Grafik dargestellt.

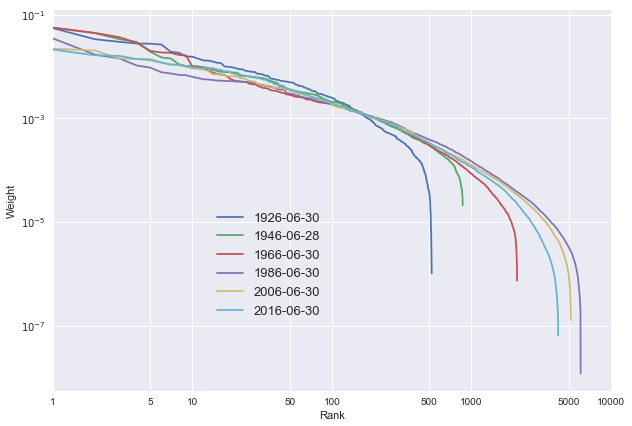
Jede dieser Kurven zeigt die relativen Marktkapitalisierungen in geordneter Reihenfolge des US-Aktienmarkts auf einer logarithmischen Skala von 1926 bis 2016. Unbeeindruckt von Krisen oder florierender Wirtschaft blieb die Verteilung der geordneten relativen Marktkapitalisierungen über die vergangenen 100 Jahre erstaunlich stabil. Konkret bedeutet dies beispielsweise, dass im US-Aktienmarkt die ersten drei Unternehmen immer mehr als 5 Prozent der gesamten Marktkapitalisierung aufwiesen. Diese grundlegende Stabilitätsbeobachtung war der Ausgangspunkt für Robert Fernholz vor einigen Jahrzehnten das Gebiet der "Stochastischen Portfoliotheorie" zu entwickeln. Mittlerweile wurde dieses Phänomen nicht nur in klassischen Aktienmärkten, sondern auch bei Kryptowährungen beobachtet.

Pfadabhängige Volatilität

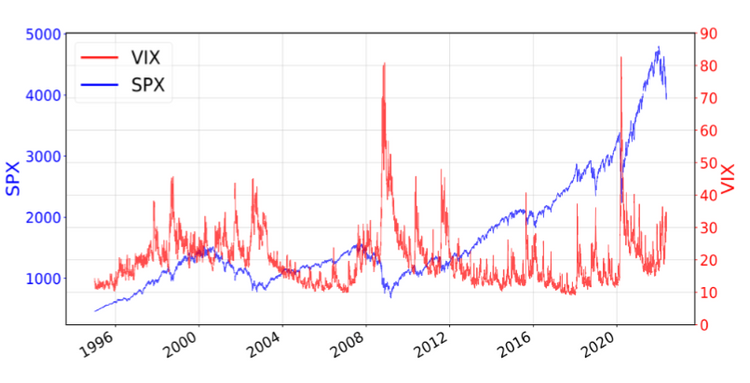
Ein zweites universelles Phänomen auf Finanzmärkten ist das Konzept der "pfadabhängigen Volatilität". Volatilität ist ein Maß für die Schwankungen der Preise von Vermögenswerten über die Zeit. Hohe Volatilität bedeutet starke Preisschwankungen, niedrige Volatilität relativ stabile Preise. Die Universalität zeigt sich hier darin, dass die Volatilität quer durch verschiedene Aktienklassen stark von den vergangenen Renditen der jeweiligen Aktien und teilweise auch ihrer eigenen Vergangenheit abhängt. Das bezeichnet man als Pfadabhängigheit, wobei der Pfad der "Weg" ist, den die Aktienrenditen oder die Volatilität in der Vergangenheit beschritten haben. Man sieht diese Pfadabhängigkeit zum Beispiel an den Spitzen des VIX Index (Volatilitätsindex des S&P 500) im Bild unten, die präzise durch vorhergehende negative Renditen des S&P 500 (Ticker SPX) erklärt werden können.

Nicht-Markovianität

Pfadabhängigkeit steht im Gegensatz zur "Markov-Eigenschaft". Letztere bedeutet, dass die Zukunft eines Systems nur vom aktuellen Zustand abhängt und nicht von dessen Vergangenheit. Was wir im Fall von Volatilität beobachten ist eine generische "Nicht-Markovianität", zumindest auf ihrem natürlichen niedrig dimensionalen Zustandsraum. Ähnliches gilt auch für die Modellierung der Kapitalverteilungskurven. Das bedeutet, dass beide Phänomene, die ausschließlich aus der Analyse robuster empirischer Marktmerkmale hervorgegangen sind und von einem Modellierungsstandpunkt vorerst nicht viel miteinander zu tun haben, auch eine mathematische Ähnlichkeit aufweisen.

Interessanterweise ist diese "Nicht-Markovianität" auch bei modernen KI-Algorithmen, wie Large Language Models (LLMs), die für ChatGPT eingesetzt werden, zentral. Da LLMs den Kontext über mehrere Sätze hinweg berücksichtigen müssen, ist eine Form der "Nicht-Markovianität" entscheidend. Informationen aus früheren Teilen des Textes werden durch "Selbstaufmerksamkeitsmechanismen" extrahiert und beeinflussen dann die weitere Textgenerierung. Ähnlich verhält es sich mit menschlicher Sprache, deren Bedeutung stark vom vergangenen Kontext abhängt.

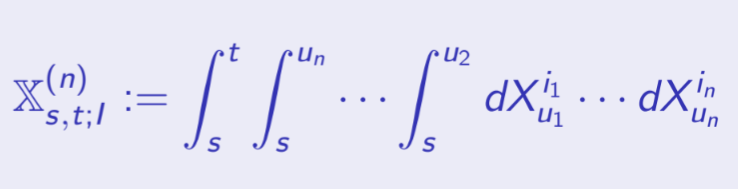
Eine andere Form moderner Machine-Learning-Techniken, die die Geschichte des Systems berücksichtigen, sind "Signaturmethoden" (signature methods). Diese werden verwendet, um die Struktur und Eigenschaften von komplexen Zeitreihen und Datenströmen, also "Pfaden", zu erfassen. Genauer gesagt ist die Signatur eines Pfades eine Sammlung von Merkmalen, ein "Feature-Set", das man durch die Berechnung von iterierten Integralen entlang der Pfadkomponenten erhält und das Zeitreihendaten kompakt und effizient beschreiben kann. Dadurch wird die Pfadgeschichte verarbeitet und Abhängigkeiten innerhalb der Daten können besser verstanden und genützt werden.

Universelle Approximationseigenschaft

Der entscheidende Grund für die steigende Popularität von Signaturmethoden ist ihre "universelle Approximationseigenschaft": Allgemeine Funktionen, die von der Vergangenheit eines Pfades, zum Beispiel von hochdimensionalen Aktienindizes wie S&P 500 oder ATX abhängen, können durch lineare Funktionen der Signatur dieser Pfade approximiert werden. Dies ermöglicht, optimale Strategien für Risikomanagement oder Portfolioselektion einfach und effizient zu bestimmen. In einer gemeinsamen Arbeit mit meiner Doktorandin Janka Möller haben wir dies mit echten Marktdaten im Rahmen von "Stochastischer Portfoliotheorie" implementiert und vielversprechende Ergebnisse erzielt.

Die universelle Approximationseigenschaft der Signatur kann auch genutzt werden, um universelle Finanzmarktmodelle zu bauen, die alle klassischen Modelle approximieren. Dies wiederum führt zu einer universellen Klasse von stochastischen Prozessen, sogenannten "Signatur-Stochastischen-Differentialgleichungen". In verschiedenen Arbeiten, die im Rahmen meines Startprojekts entstanden sind, konnten wir gemeinsam mit Francesca Primavera (Universität Wien), Sara Svaluto-Ferro (Universität Verona) und Josef Teichmann (ETH Zürich) zeigen, dass diese Modelle in die Klasse sogenannter "affiner und polynomieller Prozesse" fallen, die mich schon seit meiner Dissertation begleiten. Somit können diese Prozesse als eine weitere universelle mathematische Struktur gesehen werden, da sie ebenfalls eine universelle Approximationseigenschaft aufweisen, in diesem Fall für dynamische Modellierung mit Zufallselementen.

In jüngster Zeit gibt es auch Bestrebungen, Signaturmethoden auf Bilder zu erweitern. Die mathematischen Grundlagen dafür aufzubauen birgt verschiedene Herausforderungen, insbesondere weil die Fragestellungen an der Schnittstelle von Analysis, Wahrscheinlichkeitstheorie, Machine Learning, Algebra und Geometrie liegen. Gemeinsam mit einem internationalen Team versuchen wir das im Forschungsprojekt "Signature for images" voranzutreiben. Das Projekt wird von Ebrahimi-Fard Kurusch (Norwegian University of Science and Technology) und von Fabian Harang (BI Norwegian Business School) geleitet und vom Center for Advanced Study der Norwegischen Akademie der Wissenschaften finanziert. Ein Wunschresultat wäre ähnliche universelle Approximationseigenschaften für eine zwei-dimensionale Signatur zu zeigen, womit man mit diesen Methoden auch dynamische Modellierung von (zufälligen) Bildern und somit KI-Bilder-und Videogenerierung angehen könnte. (Christa Cuchiero, 29.5.2024)